OO_Unit1
一、架构设计迭代
1.hw1
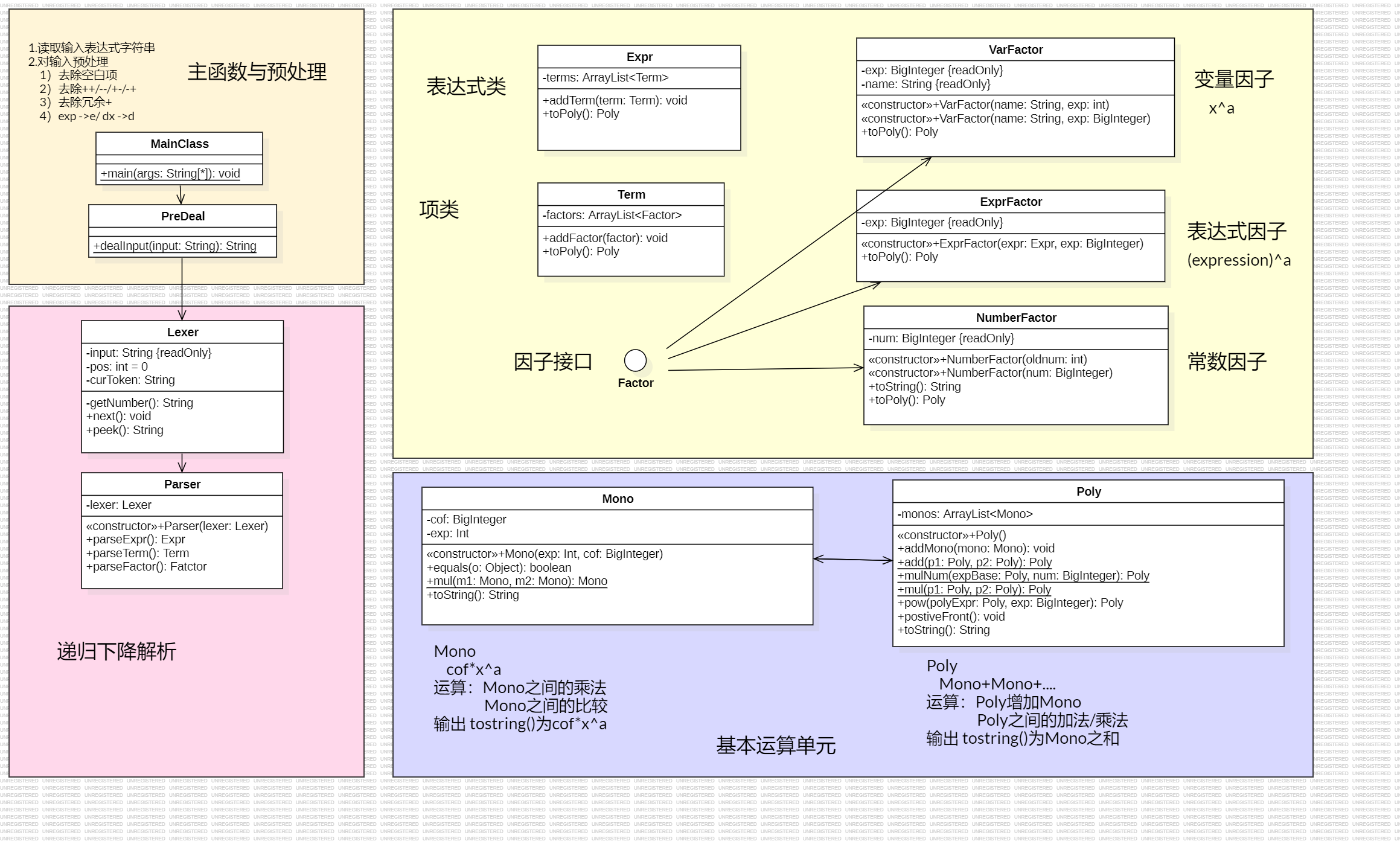
1.1 UML类图
1.2 架构分析
海量阅读往年优秀博客后(◔‸◔)后,我的架构主要仿照Unit1_training的提示以及oolens递归下降的代码仓库,如下处理:
表达式预处理
Predeal类中对输入字符串一键replaceAll
- 去除空白项
- 去除冗余++/–/+-/-+
- 去除冗余+(*+ /^+)
表达式解析
递归下降法构建Lexer类和Paser类
PaserExpr()、PaserTerm()、PaserFactor()层层深入
解析得到表达式类Expr、项类Term、因子Fatcor
因子统一接口Factor 实现类
VarFactor幂函数因子 ,定义为x^aExprFactor表达式因子 ,定义为(expression)^aNumberFactor常数因子
这里我解析Term的时候没有为其加入符号属性,而是直接遇到负号就为term加入一个值为-1的NumberFactor
基本单元定义
单项式类Mono、多项式类Poly定义如下:
$$
Mono = a*x^b\
Poly = ArrayList
$$
为Expr、Term、Fatcor写toPoly()方法,将类转化为多项式
解析完成后expr.toPoly()层层调用
基本单元运算
Mono的乘法:
1 | public Mono mul(Mono mulOne) { |
Mono的比较:当时根本没有考虑什么重写
hashcode和equal??<(`^´)>直接偷懒
return mono1.getExp() == mono2.getExp()Poly的加法1
2
3
4
5
6
7
8
9
10
11public void addMono(Mono mono)
public Poly add(Poly addOne) {
Poly poly = new Poly();
for (Mono mono : monos) {
poly.addMono(mono);
}
for (Mono mono : addOne.getMonos()) {
poly.addMono(mono);
}
return poly;
}Poly的乘法//如果是空的?这行疑问无疑为后续迭代埋下祸根……w(゚Д゚)w我的Poly为空时究竟代表为0还是没有生成呢?当时的我根本没有细想按照后者来了…….
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16public Poly mul(Poly mulOne) {
Poly poly = new Poly();
//如果是空的?"x "
if (monos.isEmpty()) {
return mulOne;
}
if (mulOne.getMonos().isEmpty()) {
return this;
}
for (Mono mono : mulOne.getMonos()) {
for (Mono monoo : monos) {
poly.addMono(mono.mul(monoo));
}
}
return poly;
}Poly的乘方调用
mul
基本单元输出
Mono的toString输出
cof*x^aPoly的toString输出
Mono之和
1.3 Bug分析
自己的bug
强测和互测都顺利通过
他人的bug
我们房间大家都很优秀是全0房捏
写完已经很不容易了,跑了跑大佬的评测机发现没什么问题,手动构造了一些极端样例,最后拜读了大家的优秀架构,只能有一个字”善!”
1.4 性能优化
cof*x^a的特殊情况缩短长度cof是0/-1/1
a是0/1
正项提前
我至今觉得我这个做法很抽象….
1
Collections.swap(monos, 0, index);//index是第一个cof为正数的mono下标
2.hw2
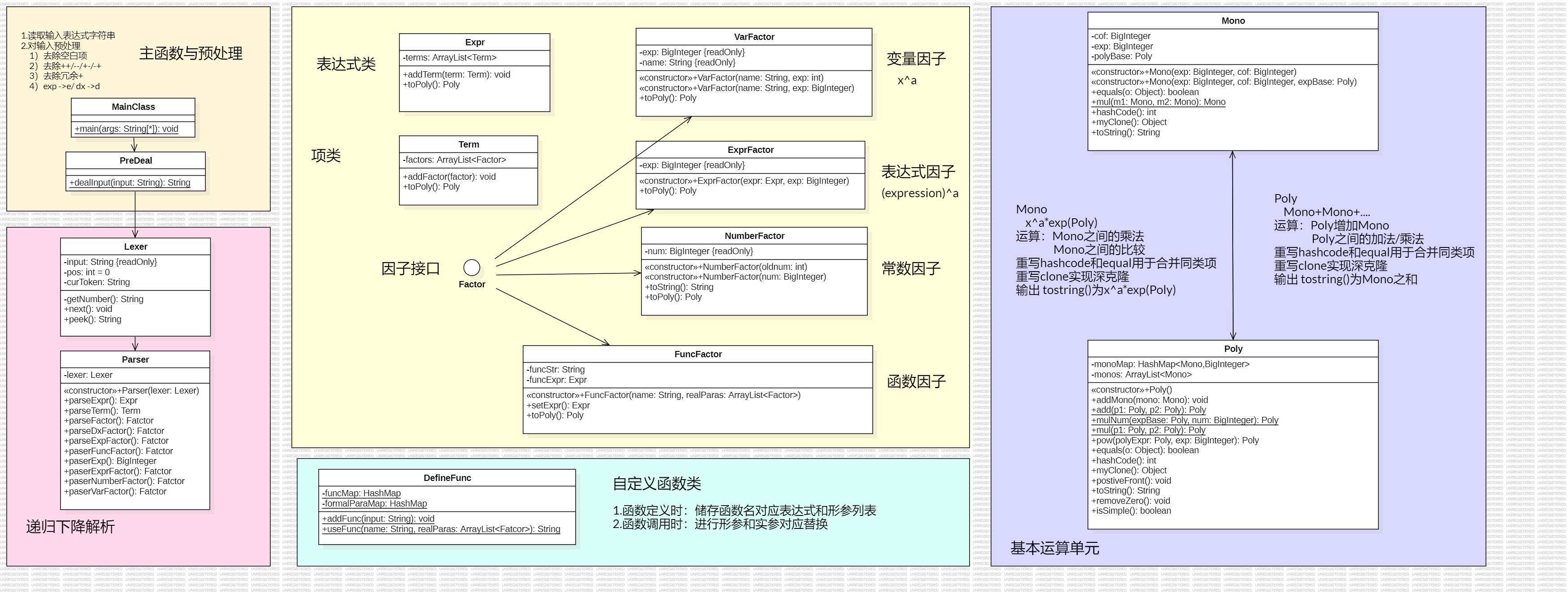
2.1 UML类图
2.2 架构分析
乍一看比去年三角函数简单,一下手发现走上了漫漫重构路(╬◣д◢)ムキー!!
本次作业共有三大需求,嵌套括号(hw1已实现)、指数函数解析、自定义函数解析
自定义函数解析:
对于自定义函数模板类Define类
- 定义时,传入函数的定义式和形参列表
- 调用时,传入
Factor实参,将定义式中形参替换实参的字符串形式(调用toString())后传出
对于自定义函数因子类FuncFactor类
- 对
Define传出的字符串解析
指数函数解析:
对
lexer、Paser进行一些修改(篇幅有限不写了)改变基本单元组成
$$
Mono = ax^bexp^c(Poly)
$$Poly和Mono至此变为互相调用的关系,需要进行大规模重构!!!!
重构之合并同类项
从网上查阅到一键重写hashcode()和equals()方法
Mono的belike:
1 |
|
Poly的belike:
等等?我用的是ArrayList<Mono> monos
如果直接一键生成,那么exp的指数Poly在调用equals()的时候不会比较每个单项式的系数,那么形如exp((3*x^2+x))与exp((x^2+x))将会被认为是相等的(゚Д゚≡゚д゚)!?
于是我们在Poly中加入对Mono系数的比较
1 | private HashMap<Mono, BigInteger> monoMap;//存放Mono以及其对应的系数 |
重构之空与零
上文提到我的惊天bug Poly为空时究竟代表为0还是没有生成呢?
按照Poly为空代表没有生成,外加上我没有remove系数为0的Mono,那么在Mono和Poly的互相深层递归调用,我应以exp内的Poly 在Poly.toString()为“0”作为返回条件,这十分复杂……
而且考虑一种特殊情况:Mono为exp(poly)^a 我要将a乘入Poly,若Poly 为空,按照Poly为空代表没有生成,那么最后结果就是exp(a),这个bug我de了一下午….
所以我最后选择按前者 Poly为空时代表为0,重写我的Poly乘法和加法,并为Poly加入removeZero()方法
重构之深克隆
在经历一系列调试的赛博闹鬼事件,我终于意识到深克隆的重要性……
所以重写Clone!:
1 | public Object myClone() { |
2.3 Bug分析
自己的bug
强测WA了一个点 指数没改BigInteger
(╯-_-)╯┴—————————————┴
他人的bug
佛系刀人但刀法了得
1-1=0的样例一刀能刀两个人我能吹一辈子!!!
强测居然连为0的数据都没有???还是不行(x)
2.4 性能优化
这是一个复杂的课题,为了偷懒我选择万无一失只优化一点点——去括号
指数函数对应的嵌套因子是否需要两侧加括号
当且仅当 exp(Poly)[^ c] 的Poly只有含单个Mono
且该Mono符合以下条件之一
$$
Mono = ax^bexp^c(Poly)
$$
- b==0 && (Poly为空 || c==0)
- b==0 && a == 1
- (Poly为空 || c==0)&& a == 1
这个只会锦上添花,永远比不优化的长度短(叉腰)
3.hw3
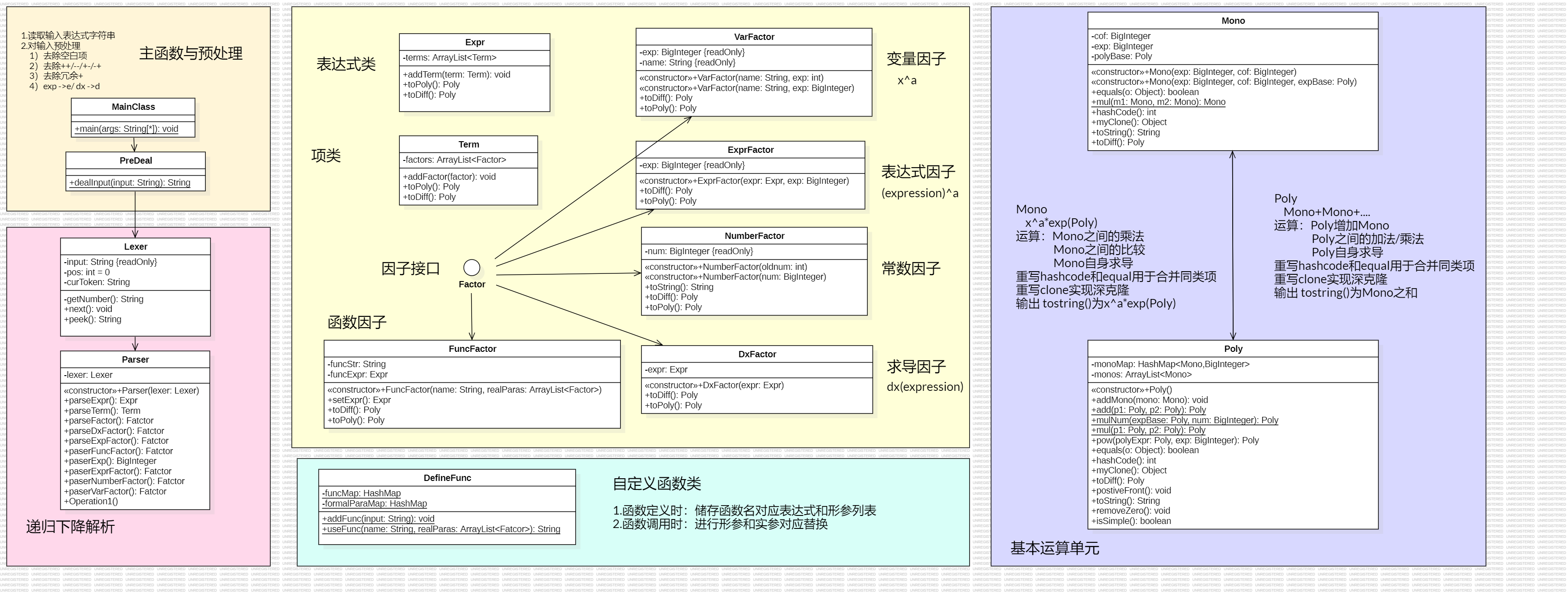
3.1 UML类图
3.2 架构分析
在第二次作业重构的基础上,很轻松水完了
本次作业共有两大需求,递归调用自定义函数(hw2已实现)和求导
为Expr、Term、Factor、Mono、Poly等写求导方法toDiff()
1 | //Expr |
3.3 Bug分析
自己的bug
强测和互测顺利通过
他人的bug
专注于hack天权星的TLE,但是因为cost没成功……
(╯-_-)╯┴—————————————┴
3.4 性能优化
没有尝试提取公因数,小小摆了
二、复杂度分析
方法复杂度
选取复杂度最高的几个方法列在这里:
| Method | CogC | ev(G) | iv(G) | v(G) |
|---|---|---|---|---|
| DefineFunc.useFunc(String, ArrayList |
9 | 4 | 4 | 5 |
| Lexer.next() | 9 | 2 | 4 | 16 |
| Parser.parseFactor() | 8 | 6 | 10 | 10 |
| Parser.parseTerm() | 6 | 1 | 5 | 5 |
| Mono.expToString() | 8 | 2 | 5 | 6 |
| Mono.toString() | 5 | 5 | 5 | 5 |
| Mono.xAndExpToString() | 3 | 3 | 3 | 3 |
| Mono.xToString() | 3 | 3 | 3 | 3 |
| Poly.isSimple() | 8 | 5 | 6 | 6 |
| Poly.toString() | 7 | 3 | 5 | 6 |
| Total | 125.0 | 128.0 | 164.0 | 192.0 |
| Average | 1.4534883720930232 | 1.4883720930232558 | 1.9069767441860466 | 2.2325581395348837 |
Lexer中用到大量的 if-else 语句来判断当前字符的类型
Paser中parseFactor也用到大量的 if-else 语句判断当前解析因子的类型
Mono.toString()方法我尽量拆成多个方法expToString()、xoString()、xANdExpToString()来降低复杂度
Poly.isSimple()为了判断exp(Poly)嵌套因子是否需要加括号,用到大量的 if-else 语句
Poly.toString()为了空串补0、正项前移,用到大量的 if-else 语句
类复杂度
| class | OCavg | OCmax | WMC |
|---|---|---|---|
| DefineFunc | 4.0 | 5.0 | 8.0 |
| DxFactor | 1.0 | 1.0 | 3.0 |
| ExpFactor | 1.3333333333333333 | 2.0 | 4.0 |
| Expr | 2.0 | 3.0 | 8.0 |
| ExprFactor | 1.3333333333333333 | 2.0 | 4.0 |
| FuncFactor | 1.0 | 1.0 | 4.0 |
| Lexer | 3.0 | 8.0 | 12.0 |
| MainClass | 2.0 | 2.0 | 2.0 |
| Mono | 1.7619047619047619 | 5.0 | 37.0 |
| NumberFactor | 1.0 | 1.0 | 5.0 |
| Parser | 2.272727272727273 | 6.0 | 25.0 |
| Poly | 2.8125 | 6.0 | 45.0 |
| PreDeal | 1.0 | 1.0 | 1.0 |
| Term | 2.5 | 5.0 | 10.0 |
| VarFactor | 1.0 | 1.0 | 4.0 |
| Total | 172.0 | ||
| Average | 2.0 | 3.2666666666666666 | 11.466666666666667 |
为了优化输出长度和计算,Mono和Poly都爆红了((
三、新迭代场景
看了去年的指导书,如果第三次作业求导算子会在自定义函数中出现,当调用该函数时,先将自定义函数表达式求导后再代入实参,bekilef(x,y,z) = dz(g(x,y,z))+dy(h(x,y,z)),那我的代码还要进行大规模的重构っ╥╯﹏╰╥c
因为我的Mono是围绕x单变量来定义的,在自定义函数的调用的时候,我只是进行字符串的替换。如果要先将自定义函数表达式求导,也就是先解析自定义函数表达式,那我还需要加入对y、z变量的解析,我的Mono可能需要加入新的数据结构
1 | HashMap<String,BigInteger> Var;//String为变量名,BigInteger为变量对应指数 |
$$
Mono = ax^by^cz^dexp^e(Poly)
$$
又将是一场酣畅淋漓的爆改……(。•̀ᴗ-)✧
四、心得体会
还记得去年说:”下一次正课再见时,一定不会这么狼狈了,我们来日方长!!!( ´͈ ᵕ `͈ )◞♡”
今年还是很菜很狼狈啊啊啊啊啊啊啊啊啊啊啊,所以今年的心得体会是连载文《失败的艺术2》
作为未来不打算从事coding行业的人,我常常在想OO课程能带给我什么
- 专业知识?年过古稀回首青春,我想我记忆中不会存在一行行看不懂的代码
- 一往无前的意志!OO都能写出来,世界上还有什么坎过不去?相信自我,发挥自我主观能动力是战胜困难的秘诀
- 沟通协作的能力!研讨课的思维碰撞,与良师益友的交流,让我感受到OO课程对团队协作力的培养,i人在自己擅长的领域也能指点江山挥斥方遒!
子曰:“学而不思则罔,思而不学则殆”,诚哉斯言!
- hw1我想着全设计好了再开码,结果一拖拖到了周五还没打开IDEA<(`^´)>
- hw2我吸取经验教训边写边构思,结果“批阅十载,增删五次”<(`^´)>
- 所以下个单元我要平衡好思考架构和下手实践<(`^´)>
子曰:“三人行,必有我师焉”,诚哉斯言!
在学业方面,我是一个沉默自闭的人,不敢提问不敢交流,总是会想
“啊?问这个问题,大家会觉得我很蠢吧”,总是害怕参照指导书balalala,总是习惯闭门造车……hw1我还勉强自己应付的来,hw2的大规模重构直接送走我了……感谢我的好舍友,看到我崩溃强撑外表下自卑自闭的心,愿意和我一起激情讨论架构,灵感的碰撞帮助我自己的思路裨补阙漏,百思不得其解的问题能够得到很好的启发与指导wwwwwww˚‧º·(˚ ˃̣̣̥⌓˂̣̣̥ )‧º·˚已经是过命的交情了!!!!!讨论区的佬们的论文,让我看到了课程组设置讨论区的良苦用心,我欣赏精巧构思的架构,避雷一些常见的bug,学习评测机的搭建(还没学会┐=͟͟͞͞( ̄ー ̄)┌),感谢各位同学的无私分享!!!!!
课程群里的助教老师和热心同学们,以有问必答的热情和有bug必de的执着,将OO22级交流群变成一个开放包容的交流平台。虽然我还是不敢在群里发言,但未来有问题或许会请教大家的(◔‸◔)感谢助教老师和热心同学的大力支持,辛苦辣!!!!!
感谢的人有好多,传道授业的课程组、助教老师们,“不耻下教”的同学们,借我测评机的老师们,默默陪伴的朋友们,良师益友助我良多!故余虽愚,卒获有所闻˚‧º·(˚ ˃̣̣̥⌓˂̣̣̥ )‧º·˚
(怎么说的和获奖感言差不多……以上排名不分先后顺序)
五、未来方向
OO课程真的超棒˚‧º·(˚ ˃̣̣̥⌓˂̣̣̥ )‧º·˚(OO上机,快乐的上机.jpg)
个人视角下的一些建议:
- 在第一次作业的时候稍微暗示一下未来迭代的方向,让我留足可拓展性的空间,避免大规模重构wwwwwww
- 公众号上或许可以再多发一些关于测评机的教程,真的好想学会啊啊啊啊啊啊啊啊啊啊

